a. (K + L)(K + M)
42.
Convert the Boolean expressions below, using the DISTRIBUTIVE
b. R + ST
law.
c. (T + X)(V + X)
a. W + ZXY
b. RS + STV + PSX
d. (J + K)(J + L)
c. DE(F + G + H)
d. X + RHS
(J + M)
a. (W + Z)(W + X)
43.
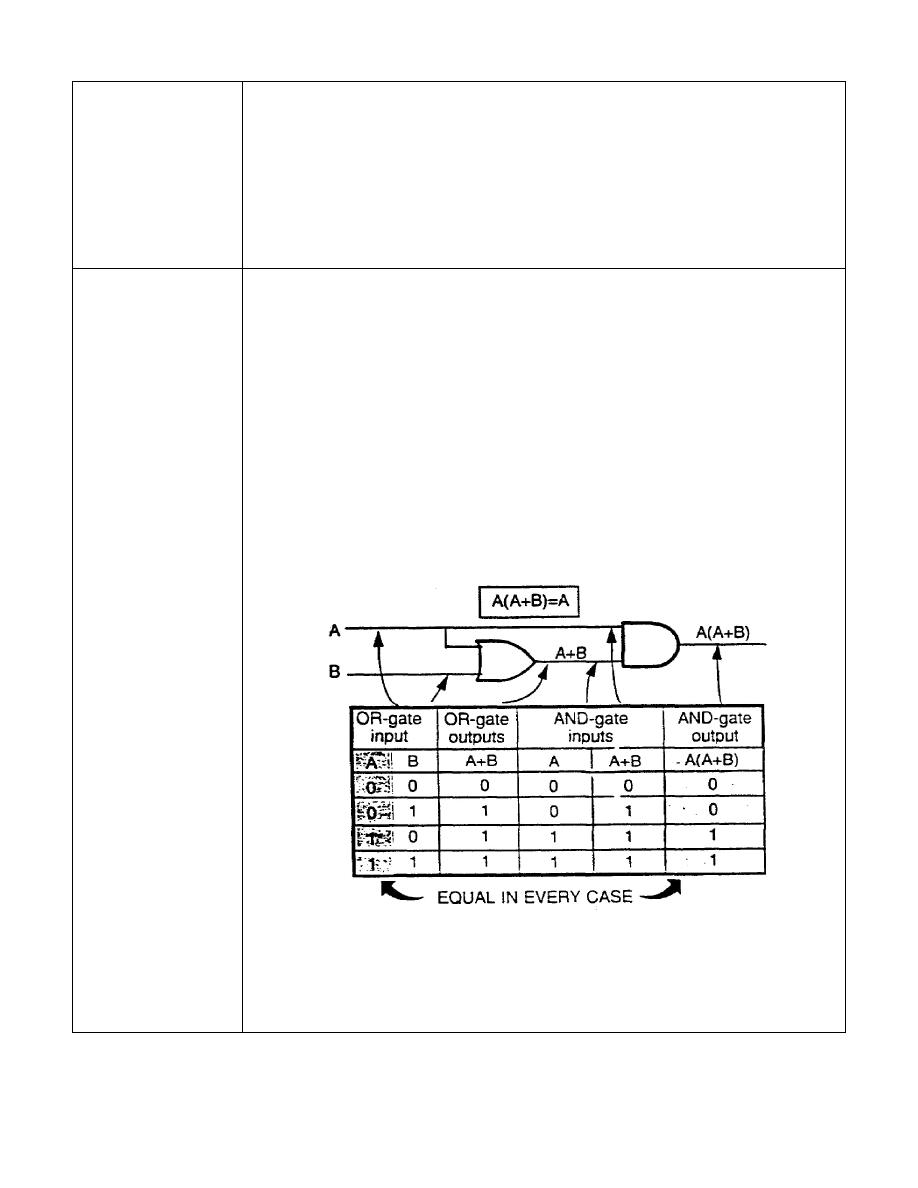
There are two equations pertaining to the law of ABSORPTION:
(W + Y)
A(A + B) =A and A+(AB) =A. How a single variable effectively absorbs
b. S(R + TV + PX)
other variables may appear confusing; however, the explanation
c. DEF + DEG +
DEH
below, which uses logic diagrams and truth tables, will prove that the
d. (X + R)(X + H)
(X + S)
equations are, in fact, valid. Since the law of ABSORPTION is often
used in simplifying Boolean expressions, carefully study the
following:
The A input column of the truth table above and the A(A + B) output
column are equal (identical) in every case; therefore, A(A + B) is
equal to A. In other words, the A variable has effectively absorbed
1-27
IT 0344



 Previous Page
Previous Page
